|
|
请使用QQ关联注册PLM之家，学习更多关于内容，更多精彩原创视频供你学习！
您需要 登录 才可以下载或查看，没有账号？注册
x
自适应分析是一个线性静态解算方案选项，适用于所有支持的求解器，该选项使用独立于求解器的高自适应分析方法在解算迭代过程中执行自动网格细化。自适应分析的主要目标是自动进行长时间、反复的多次有限元分析。网格细化取决于单元应力不连续相关联的误差估算。基于这些误差估算，在模型上标识了关键区域，这些区域随后就成为网格进一步细化的目标。( ?- T/ @: y! h) H
* Q: d$ i$ }2 x' X2 P' f& m
一旦关键区域被标识，则在内部实现局部细化。单元大小调整 schema 用于估算新尺寸。进而言之，对过渡区进行单元质量检查可消除可能在以后影响细化过程的虚假热点。: M% S5 ~8 n7 L5 [
- Z* q' Q8 D" Y/ m
注释& G, ?/ W2 {# G% }) P7 B
请记住，自适应分析确实会更改网格。因此，先于自适应解算而执行的其他解算可能包含过时的结果，并可能需要采用更新后的网格重新运行。 , r: ^* A6 ]; G9 P! n( n, j. V
+ h q# s3 C, C2 ~' }. d$ \2 |8 h% y/ F( a) x( N- [; ^. l
了解自适应解算流程* U! Y5 P' a U4 r$ p, A& A
提交作业时，会执行自动迭代分析。打开一个信息窗口，向您通知迭代分析的进度。操作完成时，您会在信息窗口中看到结果。值得注意的有以下几项：
* ]7 P( u7 m1 |: X5 R$ p0 R5 C, l9 }: O, v# U3 Z2 _
•如果原始网格的实际应力百分比误差小于您在适应性设置中指定的目标，则认为原始结果已足够，且您不会在仿真导航器中看到任何适应性结果。您也可以修改适应性设置参数并重新运行适应性解算。
8 m7 ^, s! {$ Y5 ~: k$ o
1 Q- [+ v6 P# e0 p! n* y2 g4 G8 J# x•如果原始网格的实际应力百分比误差大于您在适应性设置中指定的目标，则适应性解算节点下会出现一组新的结果，您可以通过双击结果节点来对这些结果进行后处理。 . x) k2 Y( f4 a, y! J0 u. a( y
, G4 R4 g3 Q, R, y+ w" ]! [: X运行自适应解算
$ @( M5 [ y" \8 C0 B5 Q要对特定模型启动自适应分析，则首先指定收敛准则。然后选择解算方案以应用自适应准则。
8 {, y& [/ O2 P8 R* d; I/ P0 m: l" ]! |" H. F3 Q& f/ F/ V
注释
- ~, w3 w% T& [4 C9 t% f 确定可接受限制的有效方法是在分析作业监视器中选择检查分析质量选项，然后设置自适应解算。这将向您就结果的当前质量进行指导。然后就很容易设置关于自适应运行的指导方针。
+ a1 U2 O, ?7 c2 ?3 a2 G5 k# L0 u# w- N8 P1 ~/ ~ b" c1 R
3 l: k& C: X" R" u* b! i您可以采用两种方式定义可接受误差限制：
; X. L8 }6 E x6 W: c
$ P* v& w/ n# E4 l4 q3 s/ K1 D•应力百分比误差 - 该比率反映了您对需要保留的结果的信任度百分比。
; N, f/ _5 r6 g0 b) G& B1 S; f) x. ~8 l) j/ _: n3 s6 V8 P
•应力误差偏差 - 这是一种特定的绝对误差限制，表示单元内许可的偏差。 - n8 M( h5 K- g& C; M
1 n Z! o" D# t1 v6 T. a, S" U% m
可以为自适应分析输入这两个限制中的一个或都输入；不过，将使用更严格的准则进行计算。
" s/ B: v3 m! C8 Q* ^. n5 v
6 ^' }. ~5 ?$ X; g要启动适应性解算，请在仿真导航器中右键单击适应性设置节点并选择解算。& |/ a% |* k2 g% y" F1 B
' Z& e7 c, m: n网格细化模板
+ ~0 g+ ^( U1 ~适应性决定了需要进行网格细化的区域；该信息将量化为网格中每个节点所需的多次细化。细化之后，网格得以更新。" D, C! n/ \. I1 [
' {7 _: x; X2 N
所有 2D 三角形和 3D 四面体单元均受支持自适应分析。六面体单元、楔形体单元和棱锥体单元不受支持。在自适应解算过程中，现有网格单元的细化将涉及到由匹配模板图样进行替换。需要细化的单元节点由软件标识并相应地修改。
6 Y& o6 e! n2 X. C* Y3 m
, l$ X2 ~3 A6 m4 z1 P2 U四面体网格细化
7 r7 L8 {+ T# |2 E四面体网格的细化方法是：首先抽取并细化曲面三角形网格，然后对整个实体重新生成四面体网格。 # g3 F( X5 F$ u( J/ E( O6 A) @7 t
3 n* j) g! m, q9 z1 [. J; h
三角形壳网格细化
% n9 w$ ], |$ \- F5 o' A+ l对于三角形单元，自适应分析使用三个模板进行网格细化。包含至少一个标记节点的单元边被细化。仅包含一个标记节点的单元的细化小于具有三个标记节点的单元。共享标记节点的相邻单元被称为过渡单元，并与已标识的单元按相同规则细化。. `! a" ^. c/ t
+ ], b9 H0 f) `8 ^! b对三角形/四面体网格的典型自适应分析$ ~ O% d+ F8 ~7 a" Q
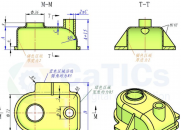
对三角形/四面体网格的典型自适应分析如以下三图中表示。从图 1 中的一个粗糙网格开始，对模型执行有限元分析，该模型提供了计算每个单元相关联误差所需的响应。基于这一评估，对网格进行更新，直到达到您指定的置信度为止。
4 v% B& b% M: F# _* B# w1 H* k: d* v0 n) g
. G4 |+ _6 Z4 s7 X, A5 n
5 Y2 k/ k1 L5 l3 {: T
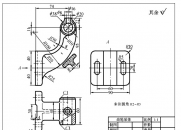
其余插图（图 2 和 3）显示基于顺序有限元分析和误差评估的第一次和第二次网格细化迭代。模型中的关键区域由其较高的网格密度来标识。; \1 N" a( k; P1 Z
) O8 j7 b8 Y. M* C6 d
1 H( u" U0 `- i% M
+ u' j0 y1 T+ A, }7 ^6 \
, ~3 Q, L {# L# G
+ @, F6 L: t7 ~; N& N" E5 w) F6 B混合网格细化- H. u0 L1 g) ? t$ g9 o
曲面网格是从网格的 3D 部分抽取的，并与网格的现有 2D 部分相结合。产生的 2D 网格得以细化，然后调用一个细化步骤来对 3D 部分进行网格划分（基于细化过的 2D 曲面）。
( w5 j5 V$ l+ K5 O. O. h6 N; f' i# ]1 C! r1 P6 i/ l# _* I: }
1 u) ]8 g; u! X; _
|
|
|小黑屋|手机版|PLM之家-专注工业软件生态建设，大模型CAD创新生态
( 沪ICP备2026005248号 )
